Random matrix theory
My PhD thesis (from the University of Melbourne) was called A geometrical triumvirate of real random matrices. With my supervisor Peter Forrester, I was working on the calculation of eigenvalue distributions and correlation functions for random real (Gaussian) matrix ensembles. Real matrices have eigenvalues that are either real or are complex-conjugate paired. This leads to eigenvalue plots that look like the following:
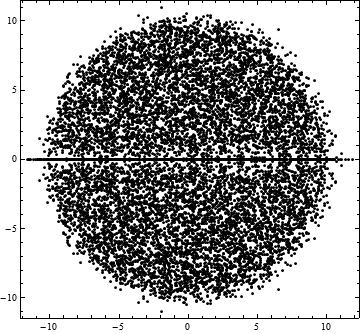
Notice that there is a line of eigenvalues along the real axis, and, if you look closely, you can see that the upper half-plane is reflected in the lower half-plane. If we now build a random matrix with complex entries or quaternion entries then we get:
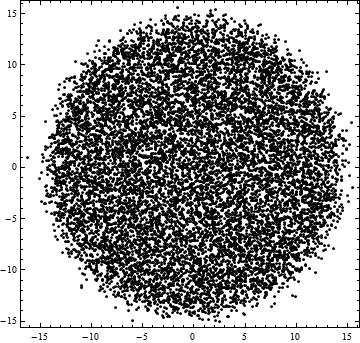
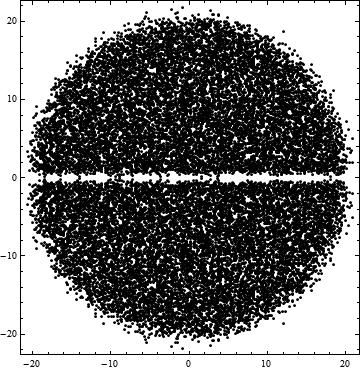
The matrix with complex entries (on the left) has eigenvalues distributed in the plane, with no further symmetry, while the matrix with quaternion entries (on the right) has eigenvalues in complex-conjugate pairs and no reals. These matrices (called the Ginibre matrices) have eigenvalues that tend to be uniformly distributed on a disk as the matrices become large.
If we now take the product A-1B, where A and B are independent Gaussian matrices, then we project the eigenvalues onto the unit sphere and we get:
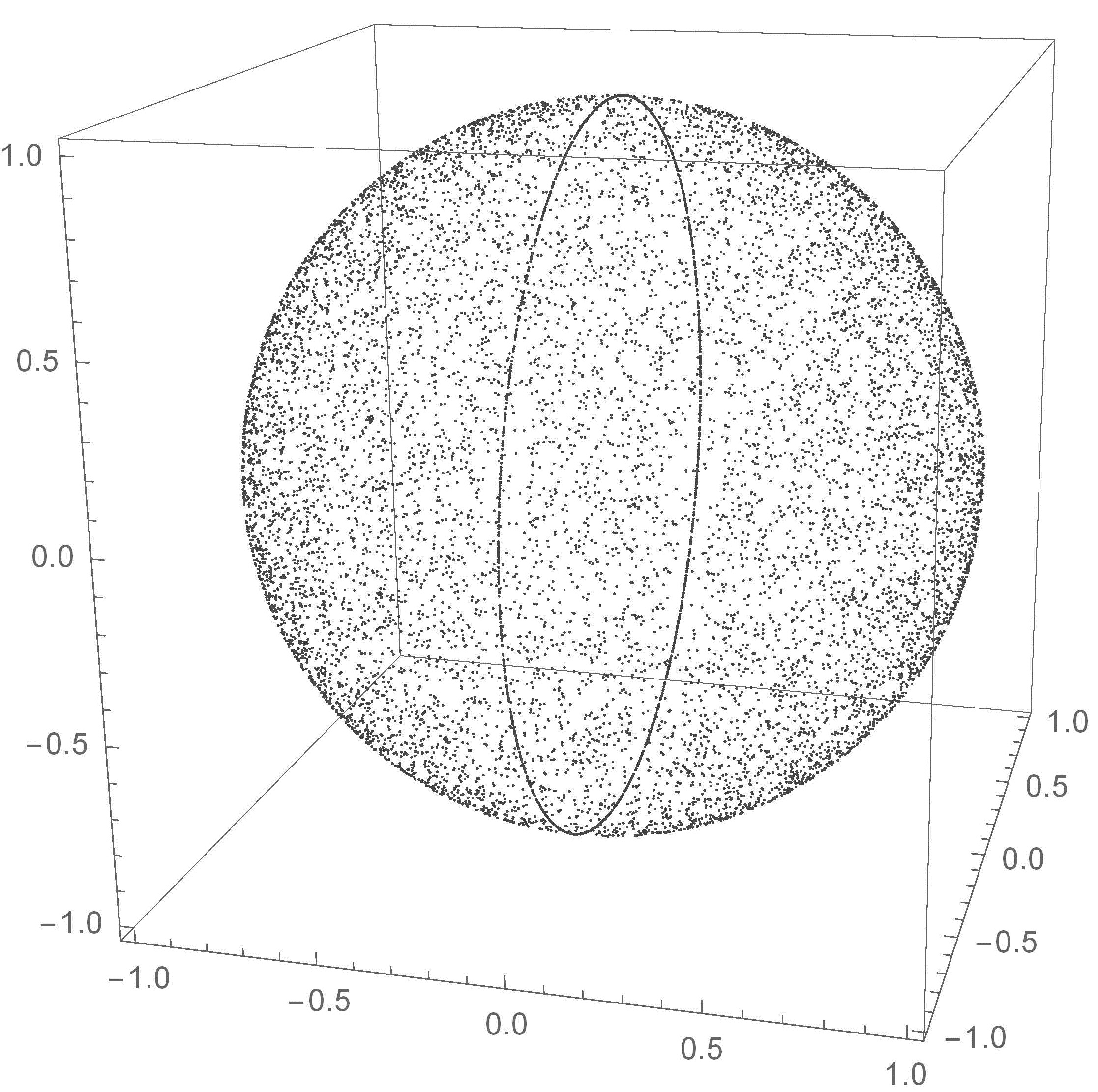
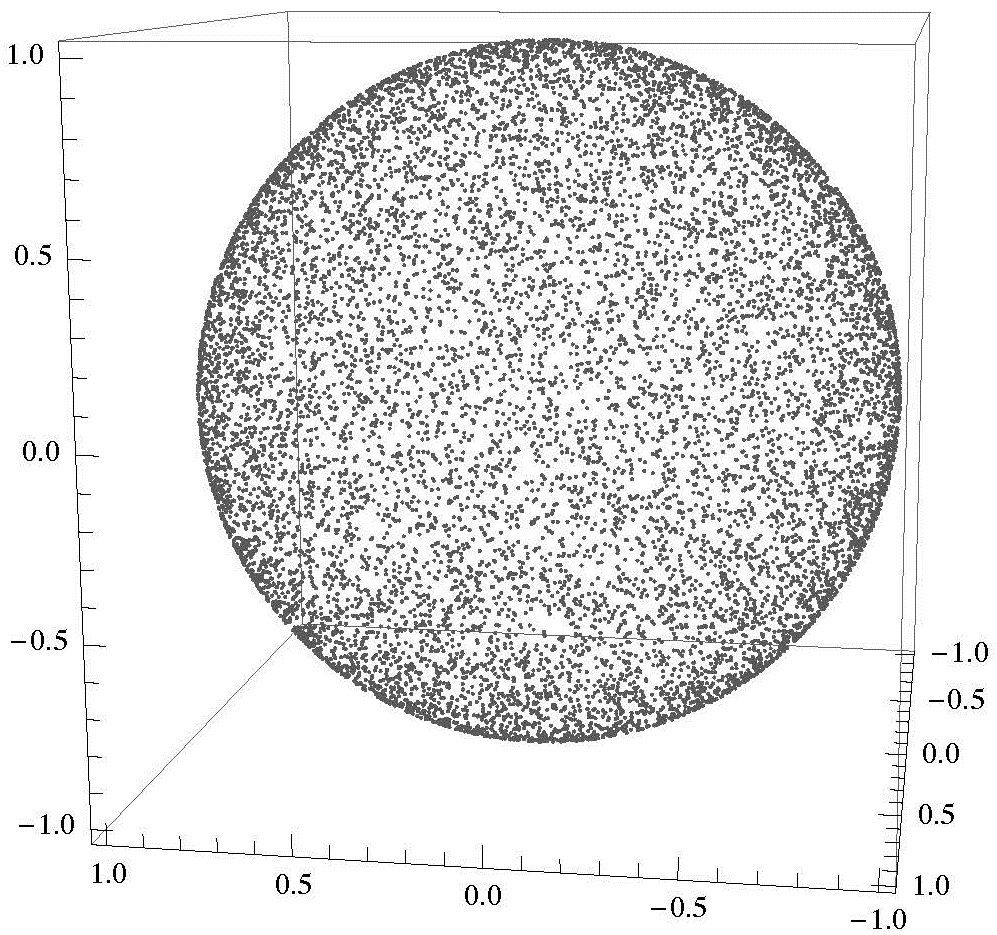
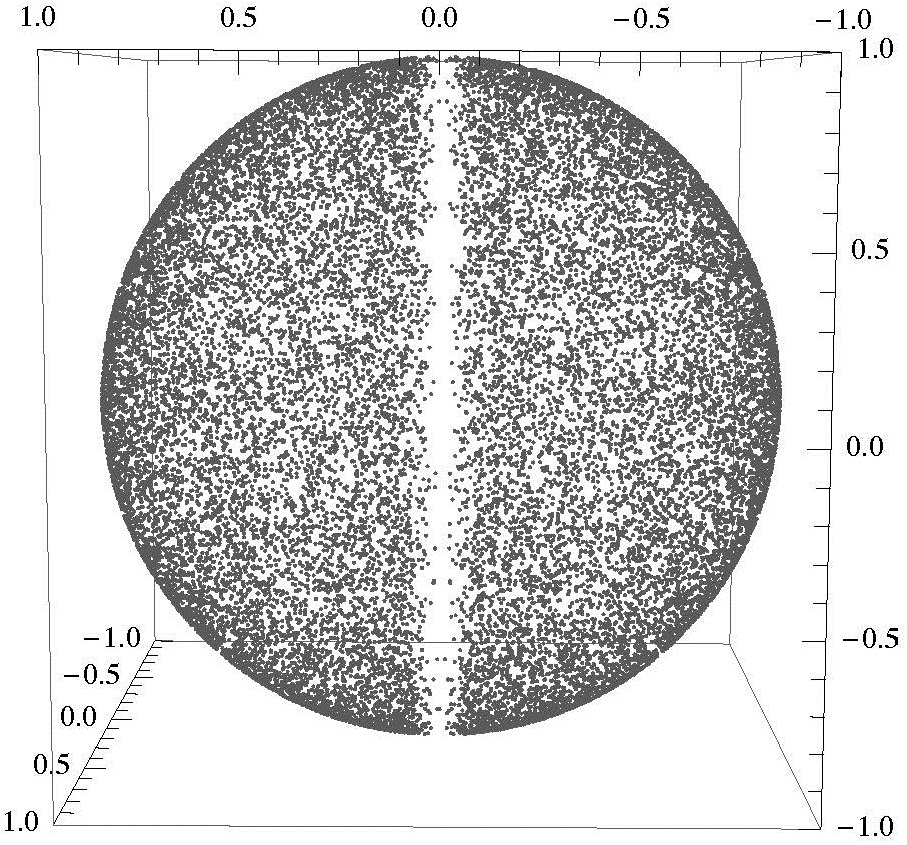
for the real, complex and quaternion matrices respectively. These ensembles are called the speherical ensembles because their eigenvalues have a uniform distribution on the sphere. We can then identify the Ginibre matrices with the plane and the spherical ensembles with the sphere, leaving just the anti-sphere or pseudo-sphere as the remaining surface of constant curvature. A natural question is: are there matrices whose eigenvalues tend to be uniformly distributed on a unit disk with negative curvature? The answer is yes; these are truncated unitary matrices.
My post-doctoral appointment at Supélec (Paris) involved working with Aris Moustakas (University of Athens) on applications of non-Hermitian random matrix theory to wireless communications. In particular, building on earlier work by Aris and his collaborators, we used tools from studies of electronlocalization (Anderson models) and magnetic flux line pinning in superconductors to study the problem of power control in wireless networks in the presence of asymmetric interference (such as home WiFi). The asymmetric case displays a richer structure than that of the symmetric networks analyzed previously, and it is these non-Hermitian matrices that I was working with. We are in the process of preparing a paper with our results. We have also investigated the use of random hopping models (such as the asymmetric exclusion process (ASEP)) to analyze dynamic situations in which the wireless data rate is now allowed to fluctuate over time, although this approach is yet to yield any results.
Recently, I have been looking at connections between random matrix theory and the zeros of the Riemann zeta function. There is a series of conjectures that the zeros of the Riemann zeta function on the critical line Re(s) = 1/2 correspond to the eigenvalues of some unknown self-adjoint operator (either exactly, or in a statistical sense). For example, it is known, up to some technical assumptions, that the leading order behaviour of the two-point function of the eigenvalues of random unitary matrices is the same as that for the Riemann zeros. High precision numerical calculations of these zeros confirm these conjectures, however proofs of these claims are still lacking, and are related to the (probably) most famous outstanding problem in mathematics, the Riemann hypothesis. The object of the current work with Peter Forrester and Folkmar Borenemann is to establish an analytical framework (using Fredholm determinants and a certain Painlevée differential equation) for the calculation of the next-to-leading order term in the eigenvalue two-point function and compare it to conjectures for the analogous quantity for the Riemann zeros.
We looked at several statistics and found good agreement with the Riemann zeros, for example
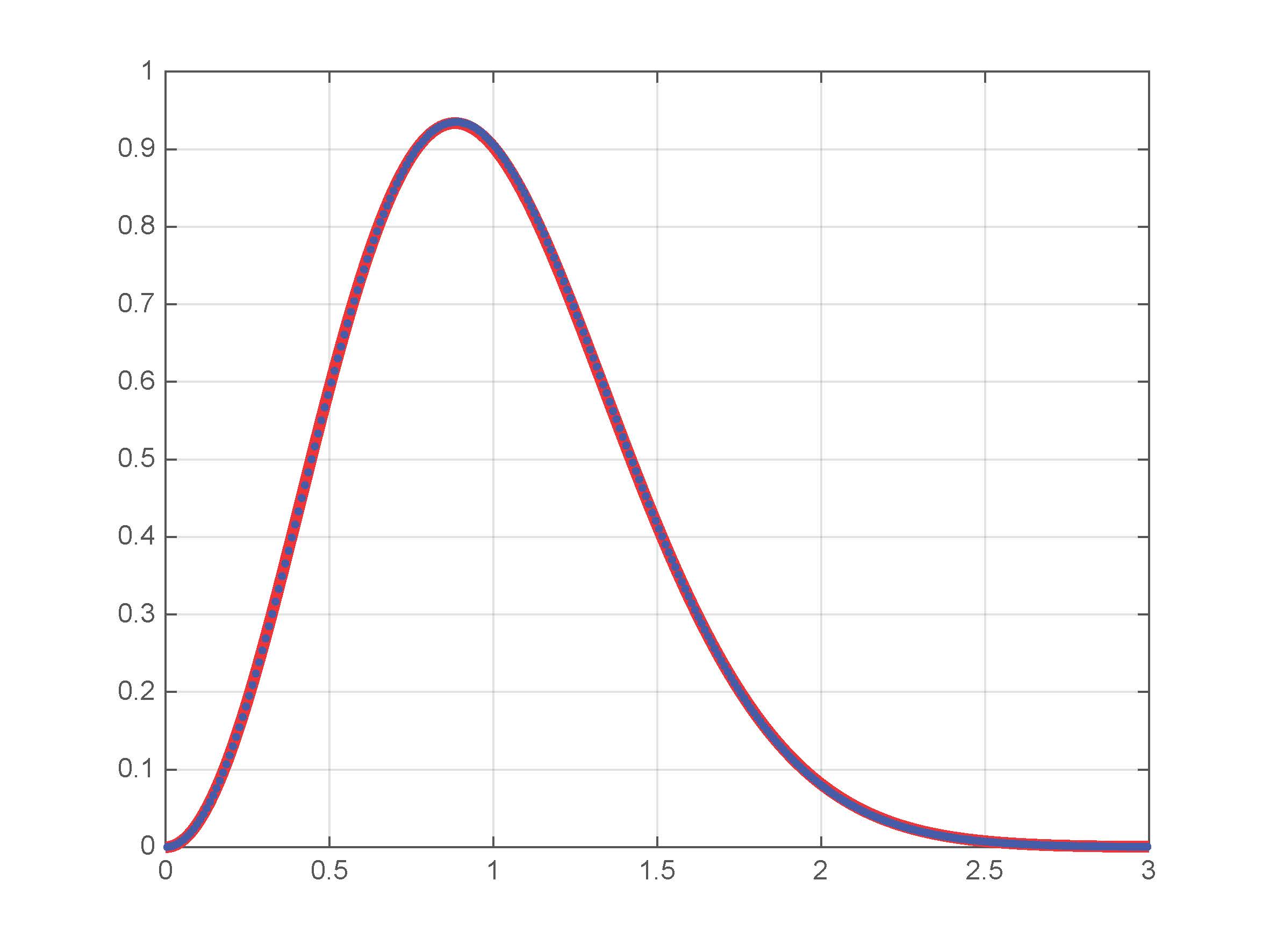
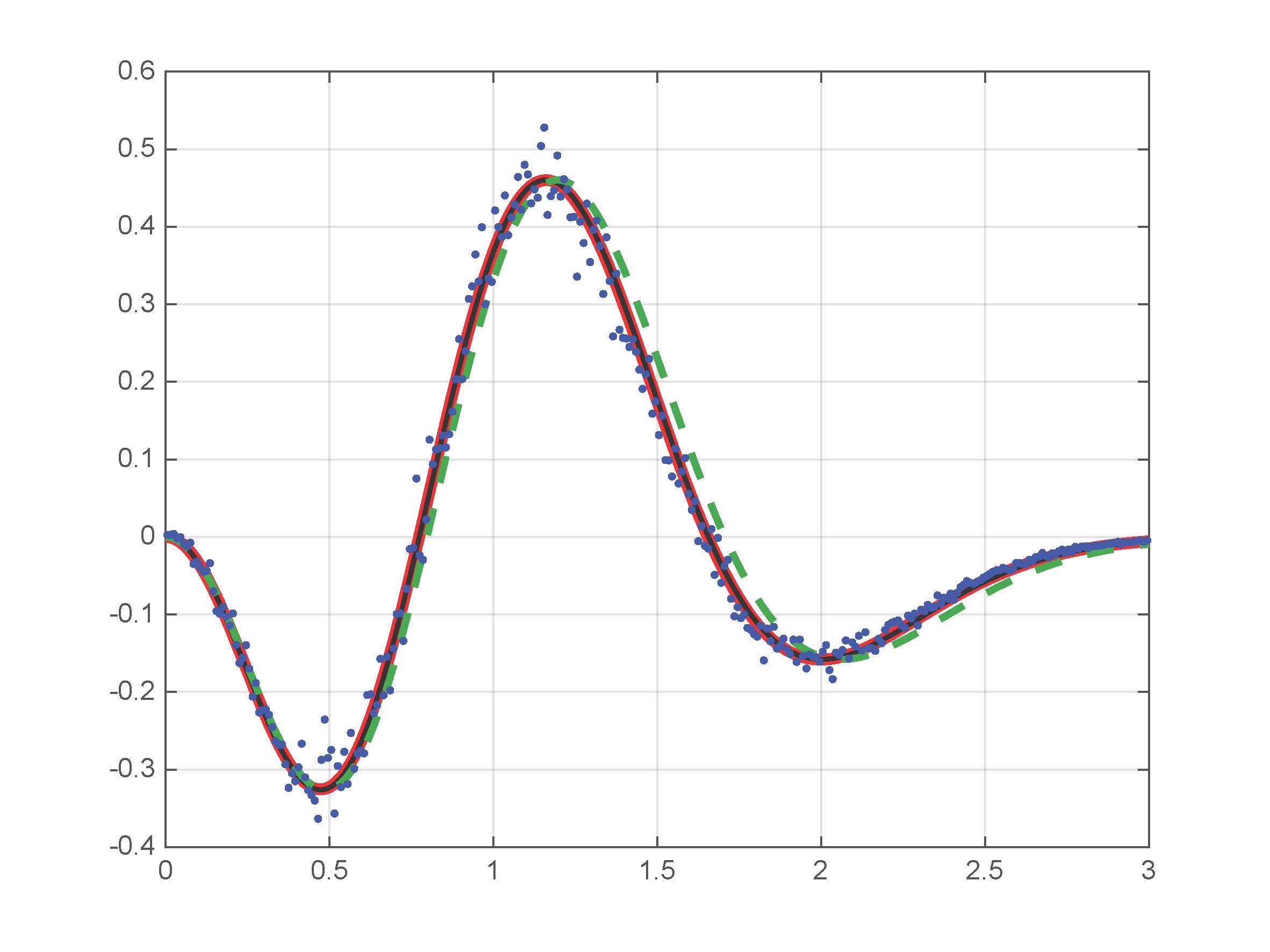
The graph on the left shows the leading order spacings for the zeros compared to the Fredholm expression and the Painlevée differential equation (they all sit on top of each other), while the graph on the right shows the first correction to the spacings. The difference between the analytic solution and the Riemann zero data is apparent on the right, however this is the largest known data set of zeros. (The dashed green curve represents a comparison to a solution which lacks a required scaling factor.)